라플라스 변환은 미분방정식을 해결하는 방식 중 하나입니다. 풀이과정은 독특하고 기존의 방식들보다 더 다양한 미분방정식을 풀 수 있습니다. 기본적인 개념은 간단합니다. t>=0인 범위에 대해 f(t)를 F(s)로 변환하는 것입니다. 이 변환 자체도 독특하긴 하지만 간단한데, 그 형태는 다음과 같습니다.

즉, e^-st를 풀려고 하는 미분방정식에 곱한 후 양의 실수 범위에 대해 정적분을 수행해주는 것입니다.
이렇게 미분방정식을 라플라스 변환을 해준 후 식을 잘 정리해서 다시 역변환 해주면 원하는 것, 즉 해를 구할 수 있게 됩니다.
몇 가지 변환 예시를 보겠습니다.

일반화를 하면 위와 같이 나옵니다. 암기할 수도 있고 암기해 두었다가 기억이 안나면 직접 적분을 수행하면 됩니다.
Example
아래의 예제는 기본적인 변환이므로 별도의 설명은 생략하겠습니다.

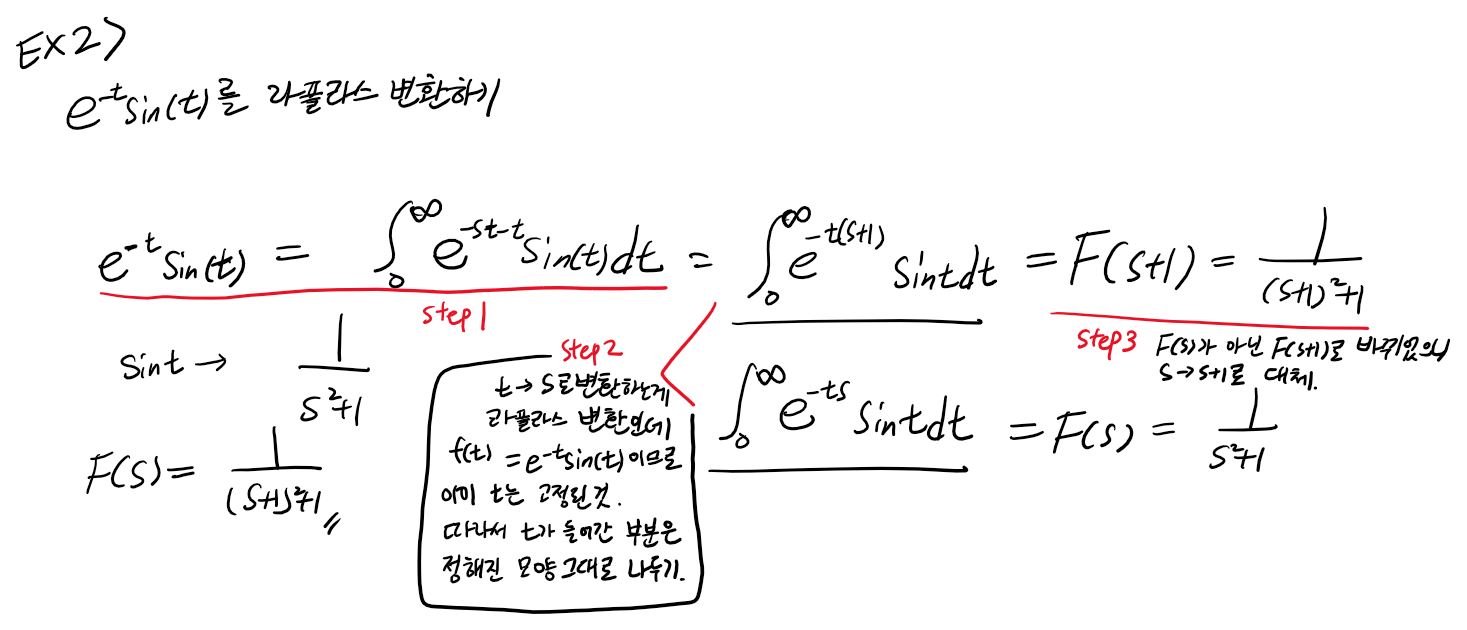
아래의 예제는 제 1이동정리로 푸는 문제입니다. 다만 라플라스 변환의 기본 내용, 즉 e^-st를 곱하고 양의 실수 범위에서 적분한다는 기본 내용으로 해결이 가능합니다.
아래의 문제에서 기본적으로 알고 있는 것은 t에 대한 식을 s에 대한 식으로 바꾸는과정이 라플라스 변환이라는 점, 그리고 위에서 찾은 공식들은 F(s)일때 성립하는 공식이라는 점입니다. 따라서 아래 문제를 풀 때, t는 t를 다른 변수로 바꾸는 게 목적이므로 t가 있는 부분들은 기존 형태가 되도록 맞추어 줍니다. 즉, e^t를 e^t+1로 바꾸면 안됩니다. 그러면f(t)-> F(s)가 아니라 f(t+1) -> F(s)의 형태가 되기 때문입니다. 그리고 남은 부분들을 s가 아닌 다른 변수나 식으로 교체하는 방식으로 해결하면 됩니다. 아래에서는 s+1이 남는데 이걸 S로 치환하면 되겠습니다. 적분은 t에 대한적분이므로 s+1을 S로 다시 표기하는 것외에는 변하는 게 없습니다.
제 1이동정리
위에서 간략하게 풀어본 제 1이동정리는 아래와 같습니다. e^at가 곱해져 있으면 F(s)가 F(s-a)로 변환되는 것입니다.

미분 형태의 라플라스 변환

y'의 라플라스 변환 과정은 아래와 같습니다. 단, e^-st * f(t)가 발산하지 않는 경우 성립합니다.
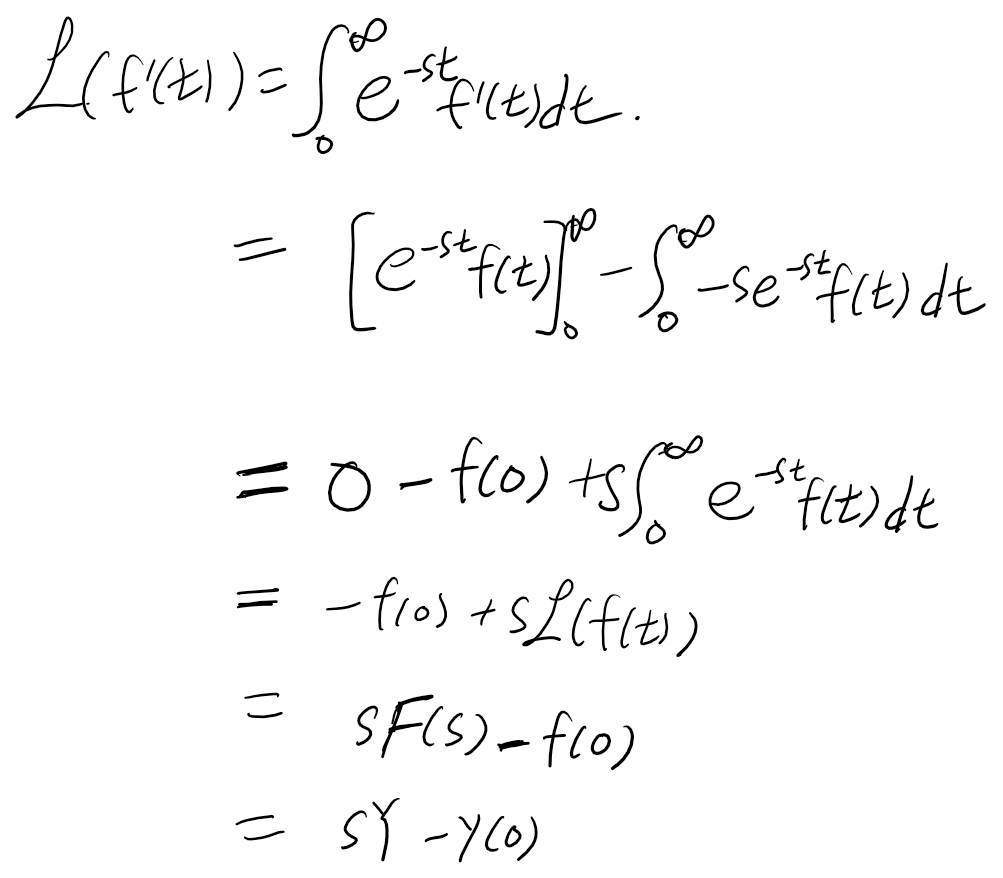
Reference:
'공업수학 1' 카테고리의 다른 글
| [공학수학 1] part A 참고 - 해의 존재성 (1) | 2023.03.15 |
|---|---|
| [공학수학 1] part D - 라플라스 변환(+ 제2이동정리, 디랙델타함수) [2/2] (0) | 2023.03.08 |
| [공학수학 1] part C - 매개변수 변환법(variation of parameters) (0) | 2023.03.05 |
| [공학수학 1] part C - 비제차 2계 ODE 미정계수법 (0) | 2023.03.04 |
| [공학수학 1] part B - 기저의 선형 독립성, wronskian (0) | 2023.03.04 |


