논리회로의 Boolean Algebra의 Theorem에 대해 다뤄보겠습니다. 세분화하면 Axioms of Boolean Algebra, single variable theorem, two and three variable properties로 나눌 수 있겠습니다. (해당 분류는 Fundamentals of Digital Logic with VHDL Design Third Edition을 따랐습니다.)
그런데 이 Boolean Algebra에서 중요한 것은 이러한 Theorem과 properties를 잘 이용하여 나중에 구하게 될 Logic Function들을 잘 최적화하는 것이 될 것 같습니다.
예를 들어, (x + y)•(y+z)•(x' + z)는 (x + y) • (x' + z)와 같습니다. 실제로 변환전의 식은 게이트만 하더라도 6개입니다. 변환 후는 and 게이트 2개, NOT 게이트 1개, OR게이트 1개로 총 4개의 게이트를 가지고 있습니다. 즉, 동일한 작업을 더 적은 cost로 할 수 있습니다. 따라서 최적화가 중요합니다. 따라서 이떄 필요한 two and three variable properties를 보겠습니다.
Two and Three Variable Properties
#참고: 아래에서의 전개과정은 정확하지 않을 수 있습니다. 기본적으로 항등식의 관계를 갖고 암기해두면 좋지만 간단하게 과정을 떠올리면 좋지 않을까 하여 변환과정을 임의로 작성한 내용입니다.
1) x + y•z = (x+y)•(x+z) - 분배법칙
[과정]
드모르간의 법칙을 적용: (x' • (y'+z'))
0,1만 있으므로 모든 인자의 쌍대로 변환: (x • (y+z) )
분배: (x•y + x•z) = x•y + x•z
다시 드모르간 법칙 적용: (x'+y') • (x'+z')
0,1만 있으므로 모든 인자의 쌍대로 변환: (x+y)•(x+z)
*참고 •이 연산 순위가 우선이므로 드모르간의 법칙을 적용할 때 • -> +인 경우 +를 우선 연산하도록 괄호를 씌움
2) x•(x+y) -Absorption
[과정]
드모르간의 법칙 적용: (x' + (x'•y'))
쌍대 변환: (x+(x•y)) = x+x•y
결합: x•(1+y)
정리: x (1+y = 1이므로)
드모르간의 법칙 적용: x'
쌍대: x
3) x + x'•y
드모르간의 법칙 적용: x' • (x+y')
전개: x'•x + x'•y'
쌍대: x•x' + x•y
정리: x•y
드모르간의 법칙 적용: x'+y'
쌍대: x+y
Example
* 예제는 Fundamentals of Digital Logic with VHDL Design Third Edition에서 참고하였습니다.
Q. f = x1x3 + x1x2' + x1'x2x3 + x1'x2'x3'을 최소화하라.
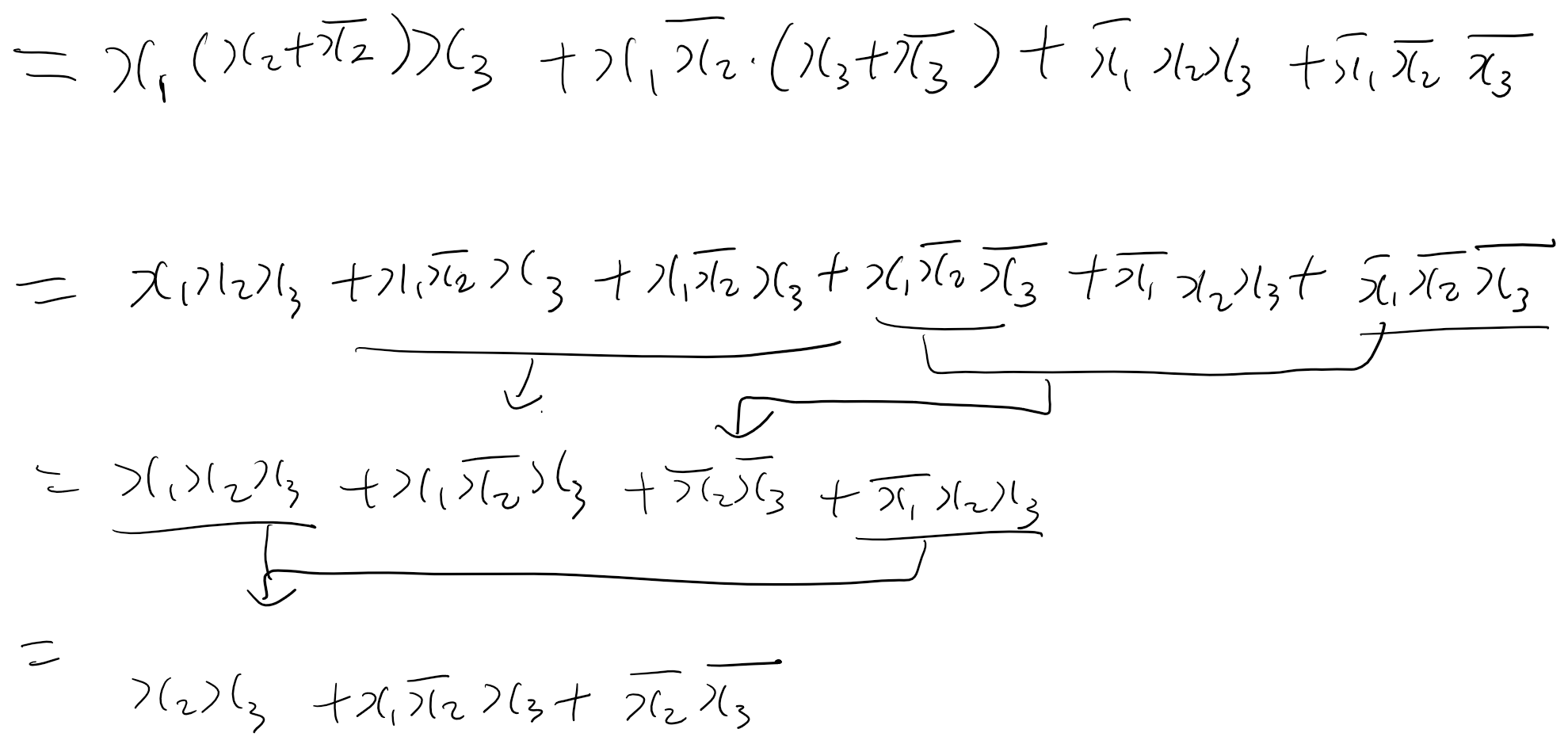
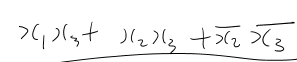
Q. 다음의 식이 성립하는지 성립하지 않는지를 보여라. x'x3 + x1x2x3' + x1'x2 + x1x2' = x2'x3 +x1x3' + x2x3' + x1'x2x3
* 두개의 input으로 이루어진 항을 3개의 input으로 바꾸어주면 계산은 많지만 적은 논리로 쉽게 해결이 가능합니다.
좌변정리:
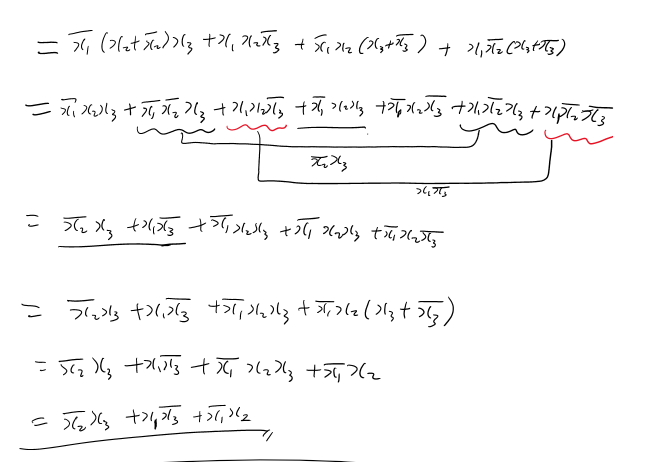
우변정리:

'논리회로' 카테고리의 다른 글
| 논리회로 - Multiplexer(멀티플렉서) (0) | 2023.05.01 |
|---|---|
| Fundamentals of Digital Logic with VDHL Design third Edition chapter 5 문제풀이 (0) | 2023.04.16 |
| 논리회로 - 복잡성(비용) 계산(complexity of Logic function) (0) | 2023.03.16 |
| 논리회로 - Karnaugh map(카르노 맵) (0) | 2023.03.16 |
| 논리회로 - Canonical form and min/maxterm (0) | 2023.03.14 |



