공진은 특정 주파수에서 큰 진폭으로 진동하는 현상을 말합니다. (공명 - 위키백과, 우리 모두의 백과사전 (wikipedia.org))
공진회로에 대해서는 어떤 주파수가 되었을때 이득(gain)이 최대가 된 경우 공진이 된 것으로 생각할 수 있습니다.
공진회로에서는 에너지 저장 소자인 L, C에 의한 영향이 없어집니다. 따라서 회로에 흐르는 전류도 전체 전압에서 저항만 고려해주면 됩니다.(각각 등가 저항, 등가 인덕터/커패시터로 구성된 단순화된 RLC회로의 경우)
어떠한 단순화된 회로에서 이득에 대해 보겠습니다.

위와 같이 R, L, C가 하나씩 직렬로 연결되면 등가 임피던스는 다음과 같을 것입니다.

전압 분배를 하면, Gain = R / 전체 임피던스이므로 다음과 같이 표현됩니다.

위의 식이 최대가 되려면 상수인 R, L, C값을 빼고 변수인 w를 조정하면 되는데 w=1 / √(LC)일때 Gain은 1이 되며 최대가 됩니다. 참고로 gain은 공진주파수인 w=1 / √(LC)에서 항상 1이되기 때문에 주파수에 따른 gain값을 아래와 같이 그래프로 그려보면 종모양의 폭이 넓어지거나 좁아지기만 하고 w = w0(공진주파수)에서의 값은 동일하게 유지됩니다.

그런데 위와 같이 기존의 방식대로 이득을 구하는 방식은 복잡합니다. 특히 병렬연결이라면 이득은 전류에 대한 관계일 것이고 직렬은 위에서 봤듯 전압을 분해하므로 전압에 관한 관계를 나타냅니다. 따라서 회로 연결 방식에 따라서 이득값을 다시 구해야하는 번거로움이 있는데, 이를 Q factor(quality factor, 양호도)를 이용하면 Q값은 회로에 따라 달라지지만 이득을 구하는 식은 모두 동일하게 표현이 가능합니다.
이득에 대한 식은 다음과 같습니다.
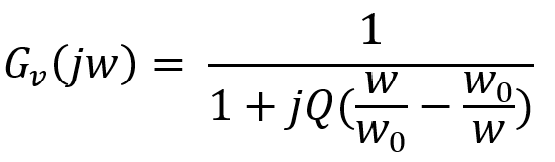
직렬일 경우 Q값은 다음과 같습니다.
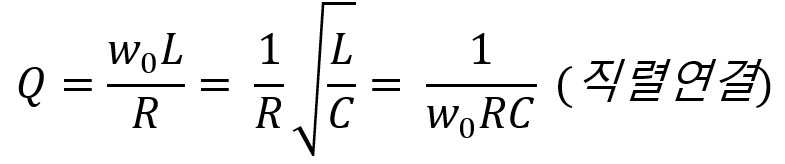
병렬의 경우 Q값은 직렬에서의 Q값의 역수입니다.
<Q값 결정 방법>

<이득값 산출>

'회로이론 > 회로이론 2' 카테고리의 다른 글
| 회로이론2 - 필터(filter) (0) | 2023.05.11 |
|---|---|
| 회로이론 2 보드선도/전달함수 (0) | 2023.05.02 |
| 회로이론2 - 변압기(transformer) (0) | 2023.04.24 |
| 회로이론 2 - 전력 (0) | 2023.03.28 |
| 회로이론2 - 최대전력 (0) | 2023.03.23 |



