이번 포스팅에서는 회로이론 교류 전원에서의 전력 파트를 다룹니다.
교류 전원에서 전력은 P=VI로 표현할 수 없습니다. 보다 일반적인 식은 S = VI*입니다.
S는 복소 전력(complex power)으로 인덕터나 커패시터들에 의한 무효전력(reactive power)까지도 포함하는 보다 일반적인 전력입니다.
이때 무효전력은 역시 실제로 전력이 소비되는 것과는 조금 다릅니다. 복소전력의 식은 real power + j * (reactive power)로 표현되는데 이 허수부가 바로 무효전력이 됩니다. 따라서 실제로 소비되는 전력을 구할 때는 굳이 필요하지는 않습니다.
따라서 실제로 소비되는 전력을 구하고자할 때는 전력의 위상이 곧 임피던스의 위상과 같음을 이용하여 아래와 같이 구할 수 있습니다.

V와 I의 곱에 cos형태가 곱해져 있습니다. 페이저에서는 실수부를 구할 때 cos값을 곱했었습니다. 1/2VmIm부분이 바로 복소전력(complex power)이고 이 복소전력의 실수부가 바로 실제로 소비되는 전력이자 일반적인 '평균전력'입니다.
아래에서 다루긴하지만 위의 식에서 1/2VmIm은 직류전원일 쓰던 전력 식과 다릅니다. 따라서 이를 동일하게 맞춰주기 위해 실횻값 개념을 이용하혀 Pavg = VrmsIrms로 표현할 수 있습니다.
1) Effective Value( RMS )
교류전원에서도 직류와 동일하게 전력을 식으로 표현할 때 나오는 것으로 '실효값'이라고 합니다.
평균전력을 먼저 전류와 관련된 변수의 제곱 * R로 표현하고자하는 목적에서부터 아래의 식 변형을 해나가면 됩니다.


이 때 나오는 Irms는 이제 다음과 같이 정리됩니다.

2) 최대 평균 전력 전달(최대 전력 전달)
부하(load)의 임피던스가 테브난 등가회로의 임피던스의 켤레복소수일때 부하에는 전력이 가장 많이 전달됩니다.
이때 부하에 전달되는 전력은 아래와 같이 구할 수 있습니다. 주의할 점은 L(부하)에서의 전압을 전압분배로 구하고 나서 허수부는 버려야한다는것 입니다. 애초에 페이저 표현을 쓸때 L에서의 전력 P를 정리하면 1/2 * (Vm^2 / R)로 정리가 됩니다. 평균전력은 허수부가 없습니다. 뒤에서 나오지만 1/2 x VI*의 실수부만 취하면 평균전력이고 VI*자체는 '복소 전력'과 관련되어 있습니다. 복소전력은 에너지 저장 소자의 무효 전력에 대한 정보까지 포함하는 전력 표현입니다.

3) 복소 전력(complex power)
복소전력의 실수부는 위에서 다룬 평균 전력으로 실제로 소모되는 전력입니다. 허수부는 무효전력이라고 하며 에너지 저장소자가 흡수/방출하는 전력인데, 인덕터는 흡수하고 커패시터는 방출합니다.
기호로는 S로 표기하며 단위는 VA입니다.
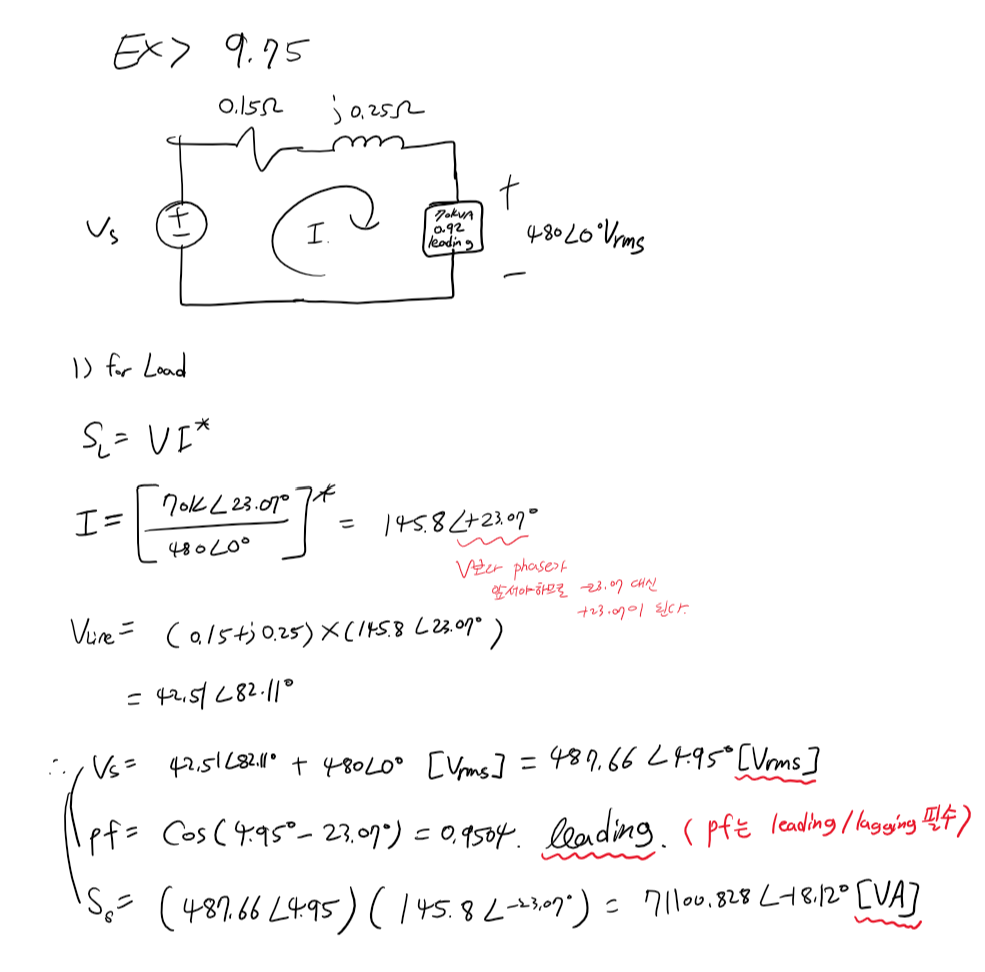
문제: Engineering Circuit Analysis 11th ( J. David irwin) 9.75
'회로이론 > 회로이론 2' 카테고리의 다른 글
| 회로이론 2 보드선도/전달함수 (0) | 2023.05.02 |
|---|---|
| 회로이론2 - 변압기(transformer) (0) | 2023.04.24 |
| 회로이론2 - 최대전력 (0) | 2023.03.23 |
| 회로이론2 - Phasor (0) | 2023.03.16 |
| 회로이론2 - 교류정상상태 분석 (0) | 2023.03.14 |



