공간상에 존재하는 이산적이거나 연속적인 전하분포들이 서로에게 영향을 주게 되면 그 공간상에는 에너지가 있을 것입니다. 만약 양 전하를 공간상에 놓는다면 같은 극성을 갖는 전하이므로 서로를 밀어내며 멀어지려할 것입니다. 즉, 에너지가 있다는 것입니다. 그러한 에너지는 다음과 같이 구해볼 수 있습니다.
이산적인 경우, 다음과 같습니다. 아래 식의 Vi는 Qi가 다른 전하들에 의해 받는 퍼텐셜의 총 합산량입니다. 각 전하가 받는 총 에너지들을 모두 합하면 계의 전체 에너지값이 나올 것입니다. 그 식이 아래와 같이 표현되는 것입니다.
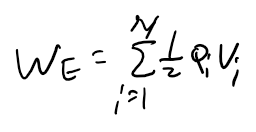
만약 전하 분포가 연속적이라면 위와 같이 시그마 표현 대신 적분을 이용해야 합니다. Q = (전하 밀도) * 부피 관계를 이용합니다. 그리고 가우스 법칙을 이용하면 전하밀도를 전기장의 divergence * ε0으로 나타낼 수 있습니다.
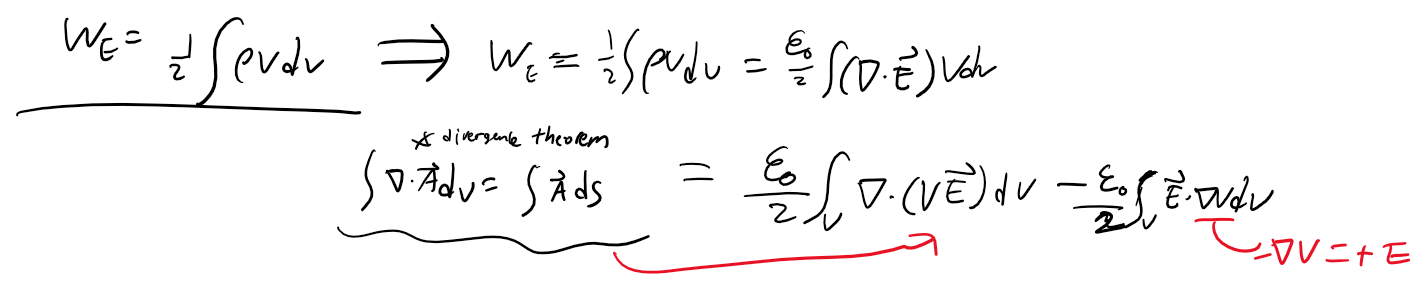
가우스 법칙을 이용하여 divergence E로 나타낸 후, 식을 전개하고 정리한 후, 첫번쨰 항에는 발산정리를, 뒤쪽 항에는
E = -gradV(전위와 전기장의 관계, 전기장과 전위의 관계 (tistory.com))의 관계를 적용하여 정리합니다. 그러면 아래와 같습니다. 그런데 아래 식은 무한한 면적에 대하여 면적분을 수행하는 것이므로 0이 되고 결국 연속적인 분포로 인한 에너지는 아래 식의 두번째 항과 같아집니다.
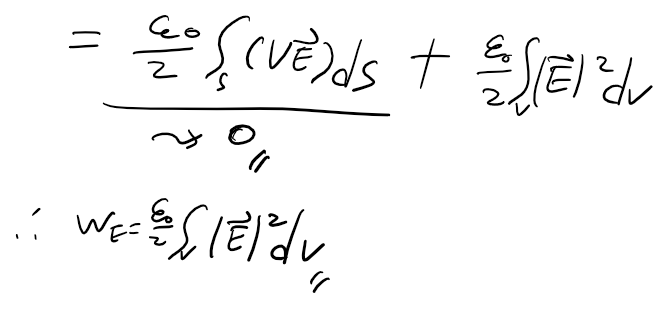
728x90
'전자기학 1' 카테고리의 다른 글
| 전자기학 Part 2(정전기학 파트) Overview (0) | 2023.04.20 |
|---|---|
| 참고사항 (0) | 2023.03.10 |
| 전기장과 전위의 관계 (1) | 2023.02.22 |
| 전위(Electric potential) (0) | 2023.02.21 |
| Gauss's law(가우스 법칙) (0) | 2023.02.21 |


