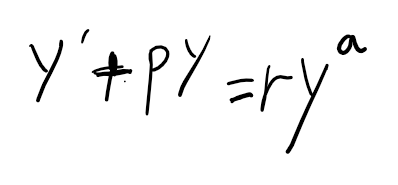
우선 위의 수식을 먼저 보고 시작하겠습니다. 선형상미분 방정식과 어떤 것이 다른지 보면 우변에 y의 지수형태가 곱해져 있습니다. r이 상수 0이 아니라면 homogeneous하지 않으며 y가 곱해져 있으므로 a가 0이 아니면 linear하지 않습니다.
이러한 형태를 베르누이 방정식이라고 하며, 선형상미분방정식은 베르누이 방정식의 specific한 case라고 할 수 있습니다.
이 베르누이 방정식은 풀이법을 바로 보고 문제를 풀어보도록 하겠습니다.
이 베르누이 방정식을 푸는데 핵심은 u = y^(1-a)를 설정하는 것입니다. 이 식을 x에 대해 미분하면 나오는 형태를 이용해서 기존의 식을 u와 x에 대한 식으로 변형해주어 y를 구하는 것입니다.
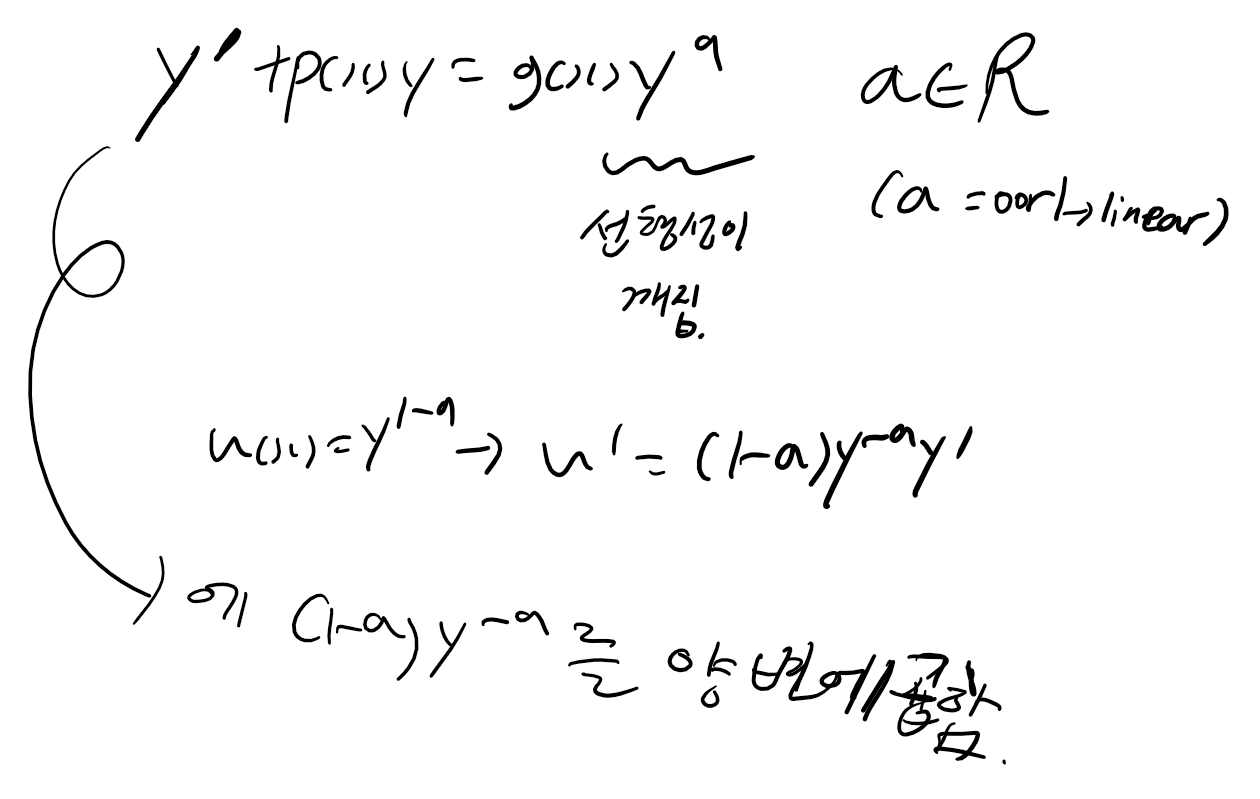
위 과정을 수행하고 나면 아래처럼 선형상미분방정식 꼴이 됩니다. 따라서 공식을 이용하면 u를 구할 수 있고 u=y^(1-a)라고 했으니 y도 바로 구할 수 있습니다.
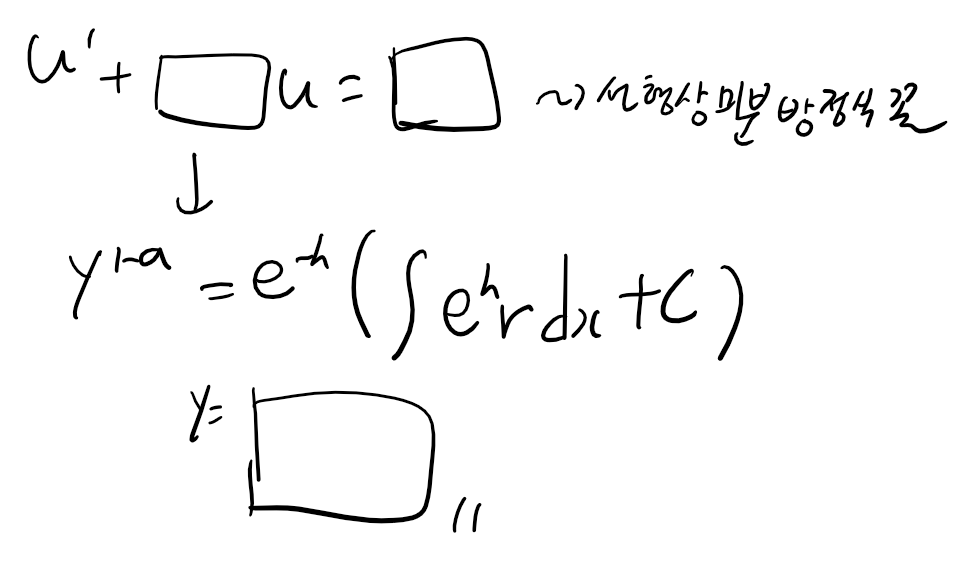
이 베르누이 방정식의 실제로 해를 구하는 과정은 선형상미분방정식과 동일하고 u=y^(1-a)를 이용하여 치환을 해주는 방식만 추가된 것이므로 따로 증명이나 일반적인 풀이과정은 생략하겠습니다.
대신 문제를 보겠습니다.
문제: xy' + y = x^2y^2d 의 해를 구하기

728x90
'공업수학 1' 카테고리의 다른 글
| [공학수학 1] part B - 상수계수를 갖는 2계 ODE (0) | 2023.03.03 |
|---|---|
| [공학수학 1] part B - 2계 제차 ODE 계수내림 (0) | 2023.03.03 |
| [공학수학 1] part A - 선형상미분방정식 (3) | 2023.03.02 |
| [공학수학 1] part A - 적분인자 (0) | 2023.03.02 |
| [공학수학 1] part A - 완전상미분방정식 (0) | 2023.03.01 |



