이전 포스팅에서 교류정상상태에서의 전력에 대해 다루었습니다. 그런데 회로이론 1에서 간단하에 문제를 풀기 위해 결과만 인용했던 교류정상상태 분석 흐름을 잠시 다시 보겠습니다.
★ 이 내용은 세부적으로 페이저를 이용한 방식이 어떻게 유도되었는지를 다루는 것으로 유도되는 과정이 특수하게 필요하지 않은 경우 일반적인 회로이론 수준에서는 넘어가도 좋습니다.
# 본 내용 전 참고사항
1. coswt = sin(wt +𝝿/2) , sinwt = cos(wt - 𝝿/2) -> t=0일때 기준으로 생각하면 쉽습니다. (ex> cos0° = sin90°)
-> 이 변환이 자주 쓰일 수 있습니다. 특히 인덕터와 커패시터에 이전 포스팅인 전력에서 보셨겠지만 I와 V가 90도 차이가 납니다.
2. cos(wt + 90°)와 같은 표기를 사용합니다. w는 각주파수로 (rad/sec)의 단위를 가지고, t는 시간입니다. 따라서 앞 항은 radian인데 뒤에는 degree입니다. 하지만 편의상 이렇게 자주 씁니다.
3. v(t) = 5cos(10t + 10°)의 교류전원이 있다고 할 때
진폭(amplitude): 5V
위상(phase) : 10°
주기(period) : 2𝝿 / w = 2𝝿 / 10 s -> 직관적으로 각주파수는와 어떠한 관계가 있을 것이라는 것은 주파수와 주기 관계를 이미 알고 있음으로, 단위가 rad/sec이므로 분모에 들어가야 2𝝿와 라디안 단위가 지워지고 sec이 분자에 들어갈 수 있다는 것을 이용하여 형태를 기억하면 좋겠습니다.
주파수(frequency): w / 2𝝿 = 10 / 2𝝿 Hz
각주파수(angular frequency): 50rad/sec
우선 페이저를 이용하는 이유는 교류 전원이 흐를 때 소자에서 전원의 진폭과 위상은 변하는데 각주파수만 안변하기 때문입니다. 따라서 전원이 v(t) = 5cos(10t + 10°)일 때, 소자에 흐르는 전류나 전압의 위상과 진폭은 어떠한 다른 방식으로 구한 다음에 이를 Acos(10t + B)에 구한 값을 대입하며 출력 값을 구해야 합니다. 이 위상과 진폭을 구할 때 사용되는 방식이 바로 페이저입니다.
[중첩의 원리 + 지수함수 방식 + 오일러 공식]
페이저는 다음의 exponential을 이용한 풀이에서 아이디어를 얻어 나온 것입니다.
아래의 방식은 원래 중첩의 원리가 복수의 전원이 있을 때 각 전원을 분리해서 하나씩 취급해도 된다는 내용입니다. 따라서 원래 아래 회로에는 전원이 한 개밖에 없는데 사실 두개의 전원이 연결된 회로에서 중첩의 원리를 적용하고자 하나를 지운 상태라고 보는 것입니다. 이렇게 생각한다면 원래의 전원이 두 개인 회로를 해석하는 문제가 되는데 여기서 핵심은 원래의 회로를 해석하여 출력 전류의 진폭와 위상을 알아내었다면 하나를 short시킨 지금의 회로에서도 해석이 끝나는 상태가 된다는 것입니다. 즉, 기존에는 풀이의 편의를 위해 두 개의 전원 중 하나를 지우고 생각했는데 지금의 교류전원에서는 두개일때 전원 두개를 하나로 묶어버릴 수 있어 해석이 쉽기 때문에 중첩의 원리를 반대로 적용하는 것처럼 생각하면 좋겠습니다.

풀이과정은 다음과 같습니다.

[페이저]

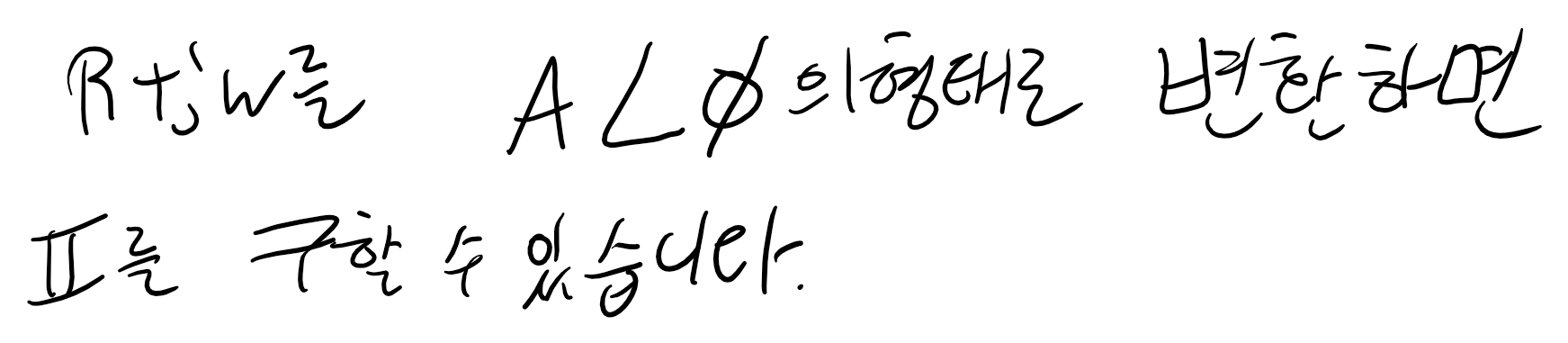
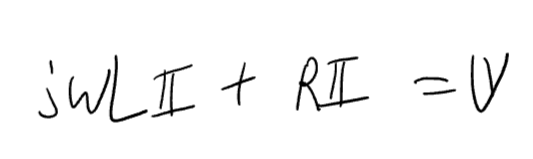
[저항 / 인덕터/ 커패시터에서의 V와 I의 위상차]
이 내용은 전력을 다룰 때 같이 다루었습니다. 인덕터와 커패시터는 전압과 전류의 위상차가 90도 나며,
임피던스가 인덕터의 경우 jwL이므로 전압은
V = jwL * I가 되는데 jwL은 진폭이 wL이고 위상이 90도인 상태이므로 전류의 위상에 90도가 더해집니다.

'회로이론 > 회로이론 2' 카테고리의 다른 글
| 회로이론2 - 변압기(transformer) (0) | 2023.04.24 |
|---|---|
| 회로이론 2 - 전력 (0) | 2023.03.28 |
| 회로이론2 - 최대전력 (0) | 2023.03.23 |
| 회로이론2 - Phasor (0) | 2023.03.16 |
| 회로이론2 - 교류정상상태에서의 평균전력 (1) | 2023.03.13 |



