divergence는 특정한 점에 대한 특성을 나타내줄 수 있는 연산자(operator)입니다. DIvergence의 역할은 어떠한 점을 둘러싸는 극소부피에서의 outward flux(바깥으로나가는 flux)를 나타내는 것 입니다.(Divergence - Wikipedia) 즉, divergence를 취한 값이 양수면 해당 점에는 source가 있어 flux가 생기고 있는 중인 것이고, 음수라면 sink가 있어 없어지고 있는 것이라는 의미가 됩니다.
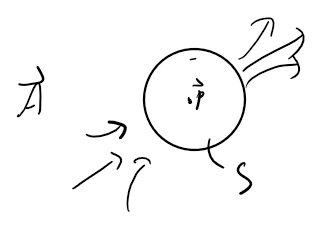
위의 그림처럼 p를 중심으로 극소 부피가 있을때 이 구의 표면으로 나가는 flux의 추세의 합산량이 divergence입니다. 합산량이라고 표현했는데 들어오는 것은 음의 outward flux라고 할 수 있으므로 이런 outward flux를 다 모아 합산한 후 나온 최종값이 divergence를 취한 값입니다. 이것의 부호에 따라 source가 있는 건지 sink가 있는건지 아무것도 없는건지(=0인 경우)를 판단할 수 있게 됩니다.
추세라고 표현한 것은 정확한 표현은 아닐 수도 있습니다만, 마치 기울기와 같은 느낌이리고 생각해주시면 됩니다. 무한히 작은 부피를 통과하고 빠져나가는 flux는 무조건 0이되므로 기울기와 같이 outward flux의 총합을 그 극소 부피의 부피값으로 나누어야 어떠한 의미나 추세를 표현할 수 있는 값이 됩니다 그리고 이것을 divergence라고 하는 것입니다.
즉, div A는 작은 부피에 대해 그 부피의 표면을 통해 나가는 flux를 그것의 부피로 나눈 값입니다.

DIvergence값 계산
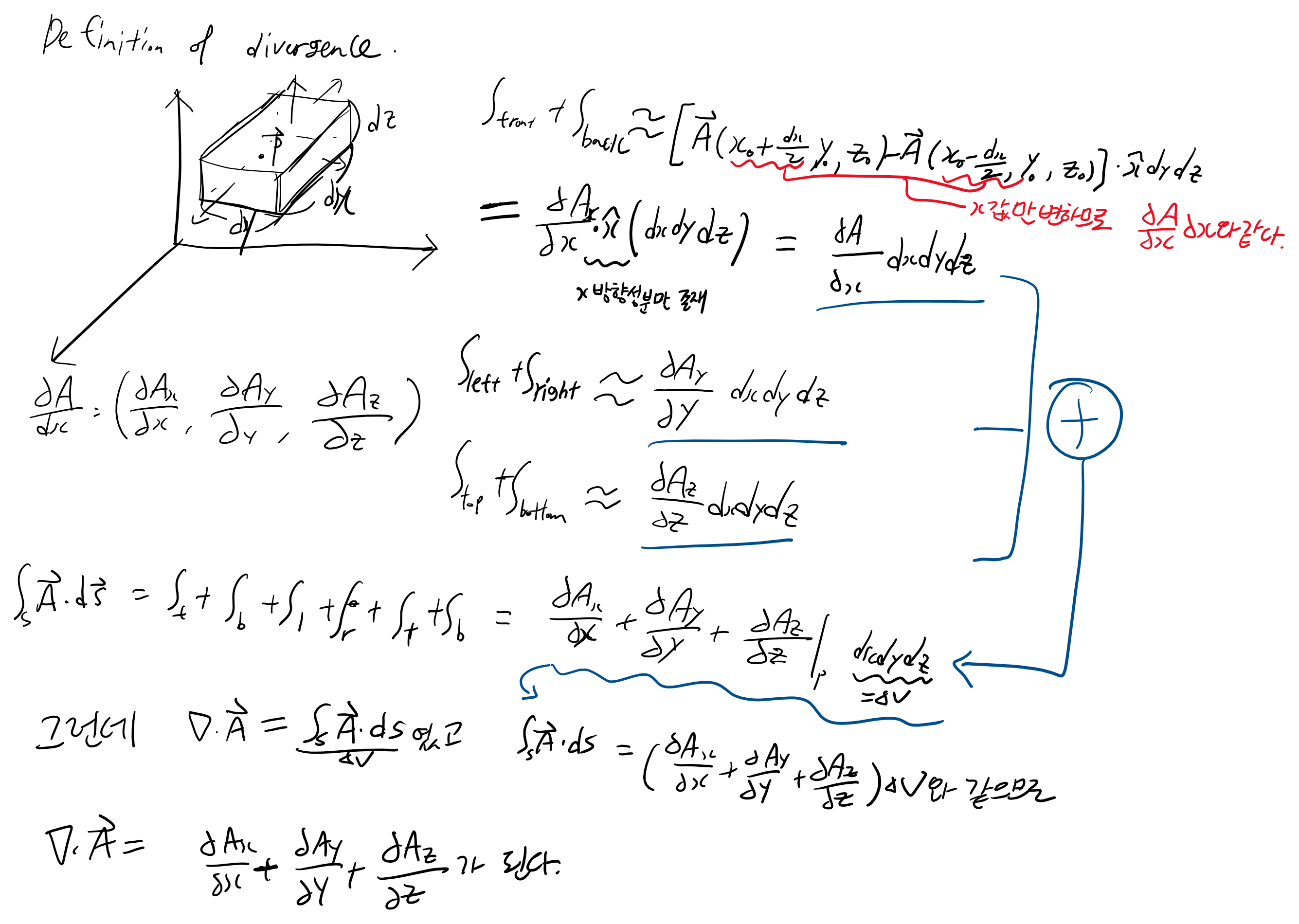
이러한 과정을 통해 벡터 A에 대한 다이버전스를 구했습니다. 그런데 위의 마지막 식의 우변을 보면 아래와 같이 내적의 형태로 표현이 될 수 있다는 것을 찾을 수 있습니다.
따라서 수식적으로 증명을 마무리 할 수 있게 됩니다.

참고로, 원통 좌표계와 구 좌표계에서는 직교좌표계로 A벡터를 변환하거나 아니면 다음의 공식을 사용합니다.
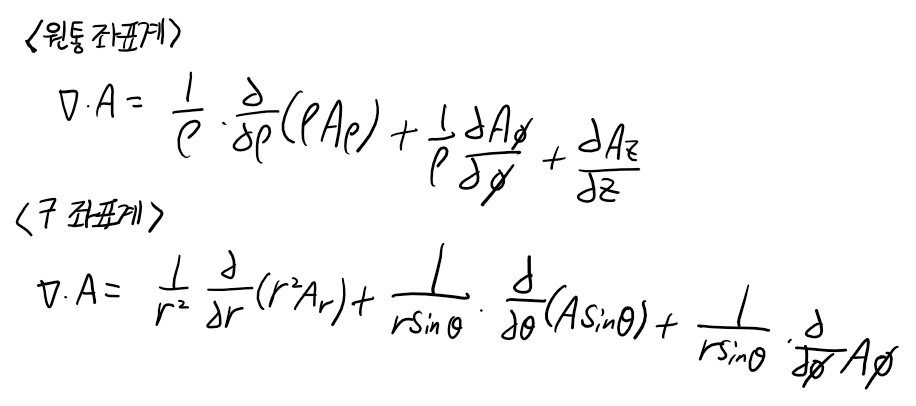
'전자기학 1' 카테고리의 다른 글
| Curl (회전) (0) | 2023.02.19 |
|---|---|
| Divergence theorem(발산 정리) (0) | 2023.02.17 |
| Directional derivative(방향 도함수) (0) | 2023.02.16 |
| Differential Length, Area and Volume (0) | 2023.02.16 |
| 전자기학1 - spherical coordinate(구 좌표계) (0) | 2023.02.06 |



