미소 길이, 넓이, 그리고 부피에 대해 알아보겠습니다. 넓이의 경우 어떠한 표면을 통과하는 flux를 계산할 때 필요하고 부피의 경우 전하의 분포를 파악하는데 사용될 수 있겠습니다. 이러한 계산들을 하다보면 어떠한 가우스 법칙이 유도되어 나오는 등 실제로 유용한 결과들이 도출되는데, 결국 전자기학에 대한 인사이트를 넓히기 위한 기반 수학이 되겠습니다.
Differential Length
[원통 좌표계에서의 differential length]
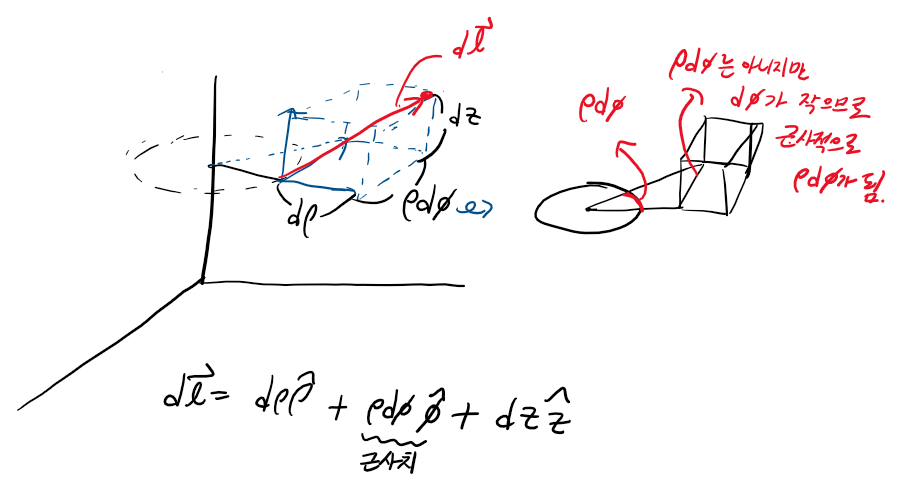
미소 길이 벡터는 원통 좌표계상에서 임의의 방향으로 뻗어나갑니다. 빨간선이 그 방향과 길이인데, 이를 해석하기 위해 원통좌표계의 성분 벡터들로 분해를 해보면 파란 점선이 됩니다. 직육면체의 모서리 중 빨간 선의 시작점인 꼭짓점에 닿아있는 모서리가 분해된 성분 벡터입니다. 즉, 미소 길이를 구할때는 해당 좌표계의 성분들로 분해를 어떻게 할 수 있는지만 보면 사실 끝입니다. 직교좌표계에서 벡터를 표현할때도 직교좌표계의 성분들로 분해한 것처럼 원통 좌표계도 동일합니다.
다만 편의를 위해서 위 그림에서도 적어두었지만 φ방향의 경우에는 근사치를 이용합니다. 사실은 부채꼴의 호와 직육면체의 모서리 길이는 다르지만 '미소 길이'의 경우에는 차이가 거의 나지 않기 때문에 같다고 생각하고 ρ * dφ로 표현합니다.
[구 좌표계에서의 differential length]
구 좌표계는 머리 속에서 바로 성분을 분해해서 생각하기는 쉽지 않습니다. 구 좌표계상에서 r방향으로 깔끔하게 뻗어나가면 간단하지만 정말 임의의방향을 향하는 경우에는 위 원통 좌표계처럼 직육면체를 그려 해석을 할 수 없습니다.
하지만 시작점이 구의 표면에 있는 아래 그림대로 3개의 성분(r, θ, φ)으로 분해하여 생각해보면 쉽게 분해해 볼 수 있습니다.
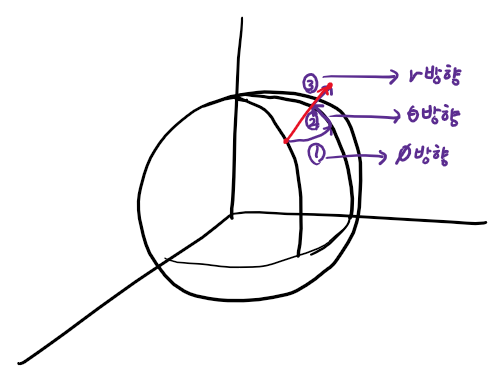
위의 그림처럼 φ방향으로 구를 따라 간 후 θ방향으로 위로 올라가고, r방향으로 바깥으로 뻗어나가면 빨간 미소 길이 벡터가 됩니다. 이렇게 분해를 했다면 1,2,3 단계 각각을 아래처럼 구해주면 됩니다.
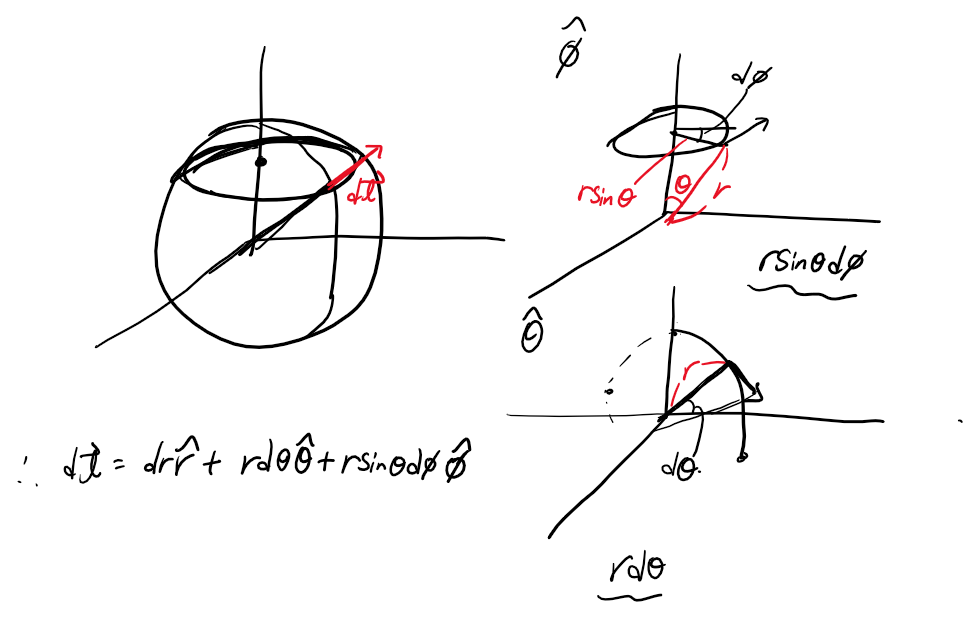
Differential Area
area도 길이구하는 방식과 크게 다르지 않습니다. 다만 면적이므로 성분을 곱해줄 뿐입니다.
[원통 좌표계에서의 differential area]
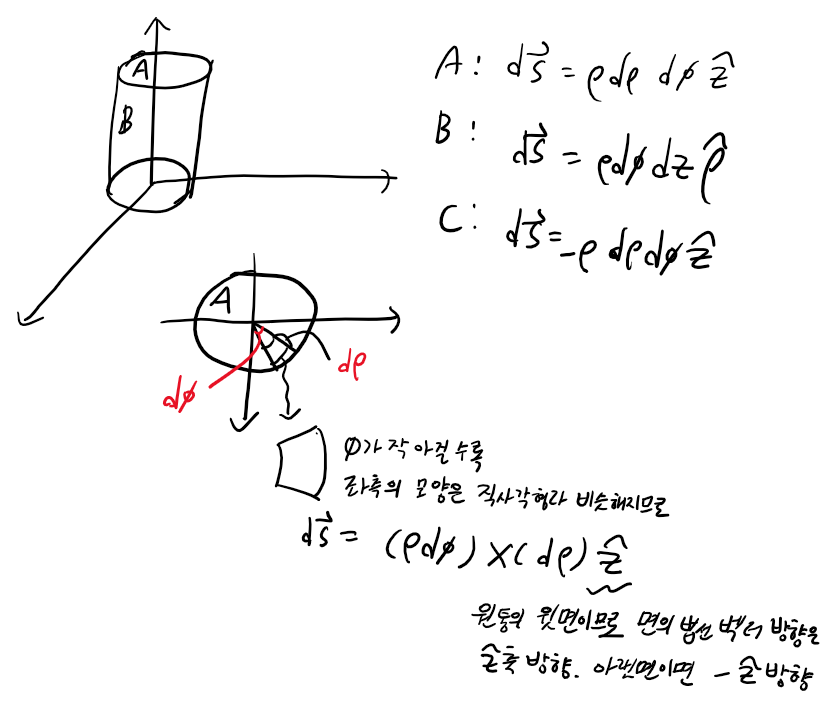
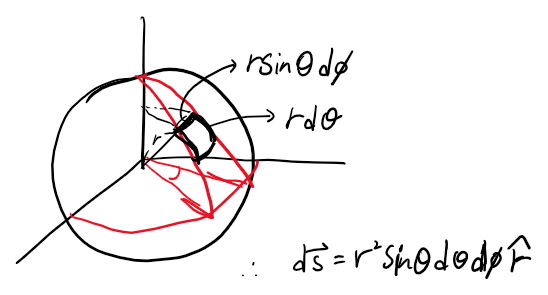
[구 좌표계에서의 differential area]
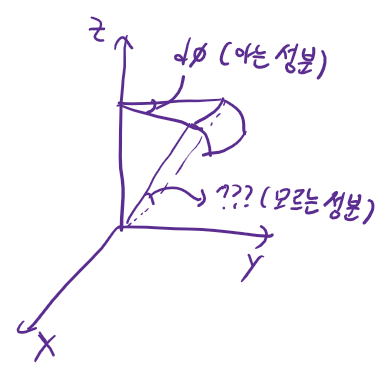
구에서는 φ성분을 구할때 sinθ가 곱해지는 걸 항상 주의해야합니다. 우리가 아는 성분과 모르는 성분을 구별해야 하는데, 각도 성분으로 알고 있는 것은 z축과의 각도와 x축과의 각도입니다. 그런데 φ방향 성분을 구하려 할 때 아래 보래색 그림의 모르는 성분으로 표현하려고 분해하면 막혀버리게 됩니다.
Differential Volume
volume구하는 것도 크게 방식 자체가 다르지는 않아 간략하게 구만 보겠습니다.
'전자기학 1' 카테고리의 다른 글
| Divergence(다이버전스, 발산) (0) | 2023.02.16 |
|---|---|
| Directional derivative(방향 도함수) (0) | 2023.02.16 |
| 전자기학1 - spherical coordinate(구 좌표계) (0) | 2023.02.06 |
| 전자기학1 - Cylindrical coordinate(원통 좌표계) (0) | 2023.02.05 |
| 전자기학1 - Vector Algrbra(벡터 대수학) (0) | 2023.02.04 |




