특정한 전하의 집합체에 의한 임의의 점에 놓인 전하가 받는 힘을 알려면 전기력을 계산할 수 있어야 합니다. 예를 들어 직선형태의 전하 집합체에 의한 영향을 구해야할 수 있습니다. 이때 작은 구간으로 나누어 계산한 후 중첩의 원리를 이용하면 전기력을 구할 수 있습니다. 단 여기서는 정전기력을 구합니다.
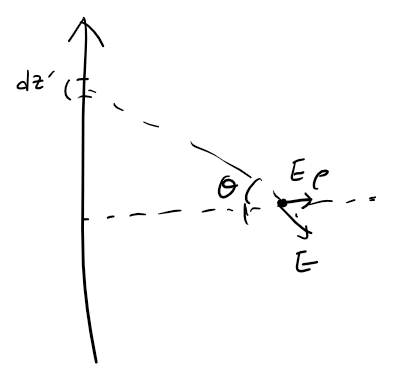
위와 같은 직선 형태로 전하들이 있을 때 dz민큼의 구간으로 나누어 이 구간이 우측의 점에 가하는 힘은 E입니다. (힘은 벡터) 그런데 이 직선이 말 그대로 길이가 무한한 선분이라면 분명 우측의 점을 기준으로 직선위에 방금 고려헀던 dz구간과 대칭인 구간이 있을 것 입니다. 아래와 같을 것입니다. 즉 ρ성분만 남습니다.
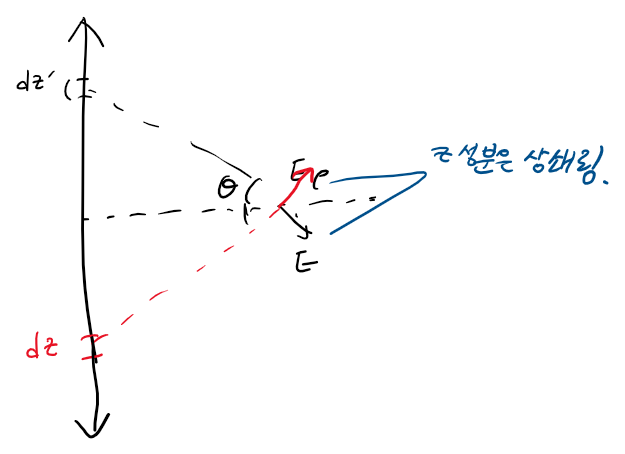
따라서, Et는 직선의 구간에서 해당 점에 가하는 힘의 ρ성분만 고려하면 되고, 이는 곧 구간이 점에 가하는 E의 코싸인 값입니다. 어차피 직선으로 확장하면 z성분은 상쇄되므로 구간을 생각할 때도 상쇄되지 않는 값만 생각할 수 있습니다.
계산은 쿨롱의 법칙에서 전하량 Q만 전하밀도 * 구간의 길이로 하면 됩니다. 전하의 선 밀도에 선 길이를 곱하며 전하량이 되므로, 원통좌표계 상에서 아래와 같이 표현되고, 이를 적분을 해주면 특정 점에서의 전기장을 구할 수 있습니다. 그점에 전하가 놓여 있는 상황이라면 그 전하가 받는 전기력을 구할 수도 있습니다.
마지막 줄의 식을 보면 거리가 멀어질수록 분모가 커져 전기력이 줄어들 것임을 알 수 있습니다.

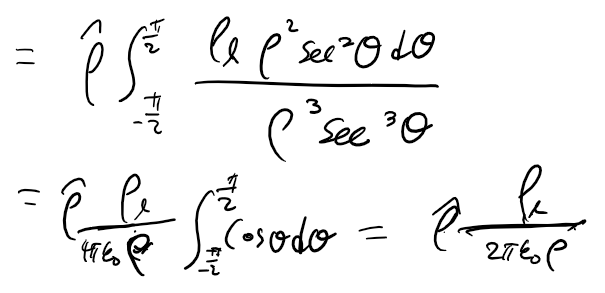
<면>
직선에 대한 전기력을 봤으니 비슷하게 면에의한 전기력도 구할 수 있습니다. 아래와 같이 원형으로 생각하면 역시 대칭성에 의해 다른 성분은 전부 상쇄되어 위로 향하는 성분만 남습니다. 만약 정사각형을 선택했다면 중심으로 부터의 길이가 다 달라 성분들이 상쇄가 되지 않고 더 복잡해질 것입니다.
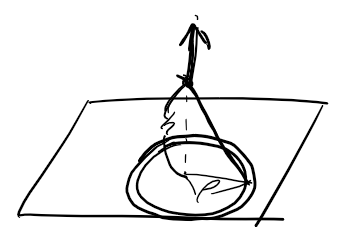
계산은 아래와 같습니다. 전반적으로 유사한데 면에 고르게 분포하다보니 미소 구간 대신 미소 면적이 되고, 편의를 위해 원을 선택했으니 미소 면적은 ρdρdφ로 계산하면 됩니다.
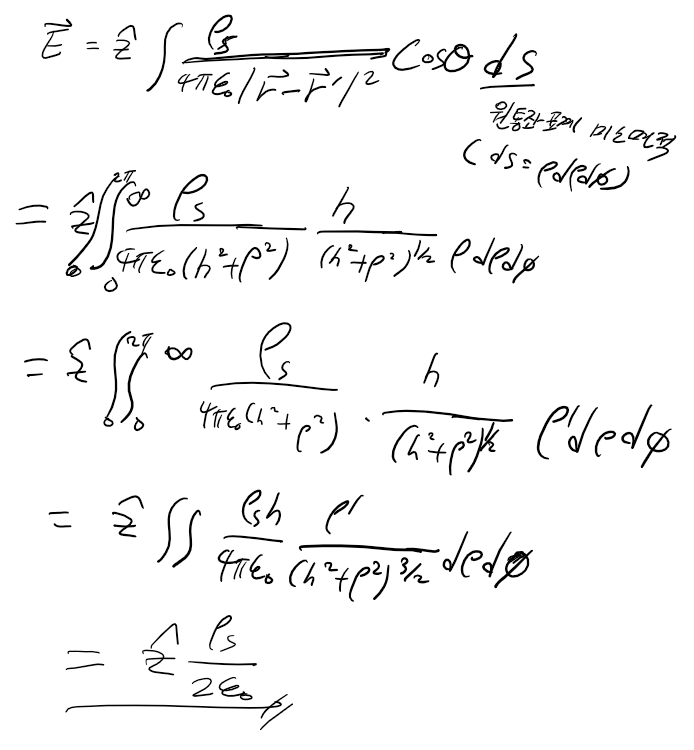
<부피>
부피는 결과만 보겠습니다. 마치 한점에 있는 것처럼 중심으로부터의 거리에 따라 세기가 결정됩니다.
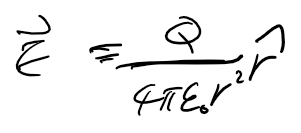
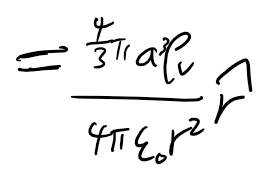
참고: 쿨롱의 법칙으로부터 전기장을 구하는 식을 벡터 표현으로 나타낼 수 있습니다. 이번에 다룬 내용에서처럼 전하들이 '많을'때, 모두를 원점에 둘 수 없고, 하나가 아닌 여러 개이므로 전기장이 선형적으로 중첩되는 원리를 이용해야 합니다.
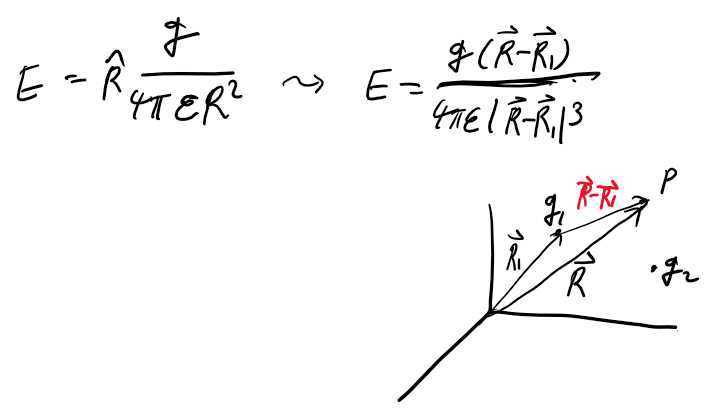
특히 하나만 있으면 원점을 그 위치로 옮기면 되지만 여러개일 때는그럴 수 없으므로 P에 대한 위치벡터와 전하 q에 대한 위치벡터를 이용하여 아래와 같이 표현해줄 수 있습니다.
'전자기학 1' 카테고리의 다른 글
| 전위(Electric potential) (0) | 2023.02.21 |
|---|---|
| Gauss's law(가우스 법칙) (0) | 2023.02.21 |
| Laplace operator(Laplacian, 라플라시안) (0) | 2023.02.20 |
| Curl (회전) (0) | 2023.02.19 |
| Divergence theorem(발산 정리) (0) | 2023.02.17 |



