가우스 법칙은 특정 영역에 대한 전하량과 flux간의 관계입니다. 식으로 표현하면 아래와 같습니다.
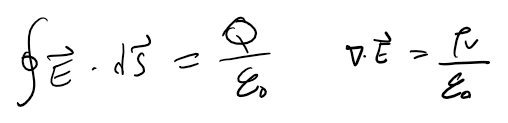
좌측의 식과 우측의 식 모두 가우스 법칙이라고 할 수 있습니다. 우측의 식은 일종의 변형이고 좌측의 식이 일반적인 표현입니다. 식의 의미는 아래와 같이 어떠한 영역에 대해 표면에서의 outward flux가 내부의 전하량에 비례상수를 곱한 값과 동일하다는 것입니다. (비례상수를 1/ε0라 했을 때)
outward flux는 전기장 벡터를 면적분 한 것과 동일하므로 첫번째 이미지와 동일한 식이 나오는 것입니다.
그런데 이 outward flux를 면적분한 값과 동일한 값은 divergence의 면적분과도 동일했습니다. 즉 영역 내부의 source와 sink의 발산정도를 합산한 것이 표면에서의 flux를 합산한 것과 동일했었습니다. 따라서 아래의 식도 성립하게 됩니다.
그러면 전기장의 divergence는 부피당 전햐 밀도를 ε0로 나눈 것과 같아집니다. 그래서 가장 위에서의 우측 식이 유도되는 것입니다.
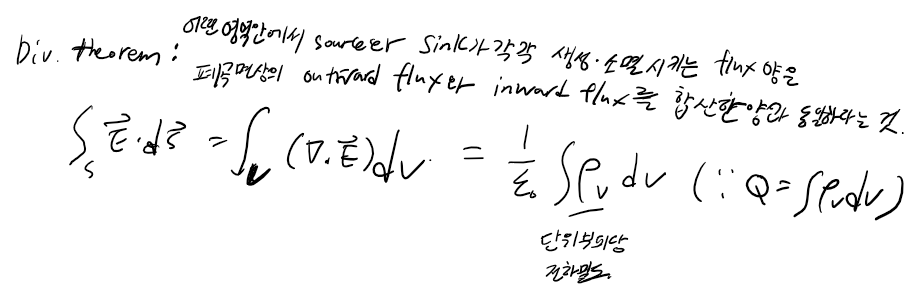
가우스 법칙을 이용한 전기력 계산
가우스 법칙을 이용하여 전기력을 계산할 수 있습니다. 아래에서 전하가 점으로 존재할 때, 선으로 존재할때, 면 또는 부피에 대해 균일하게 분포할 때에 대해 전기력을 계산합니다.
[점 전하]
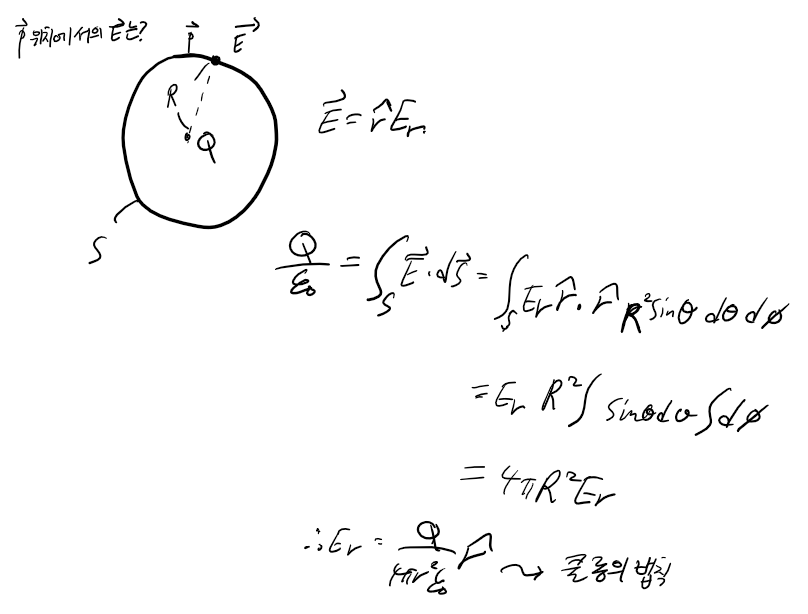
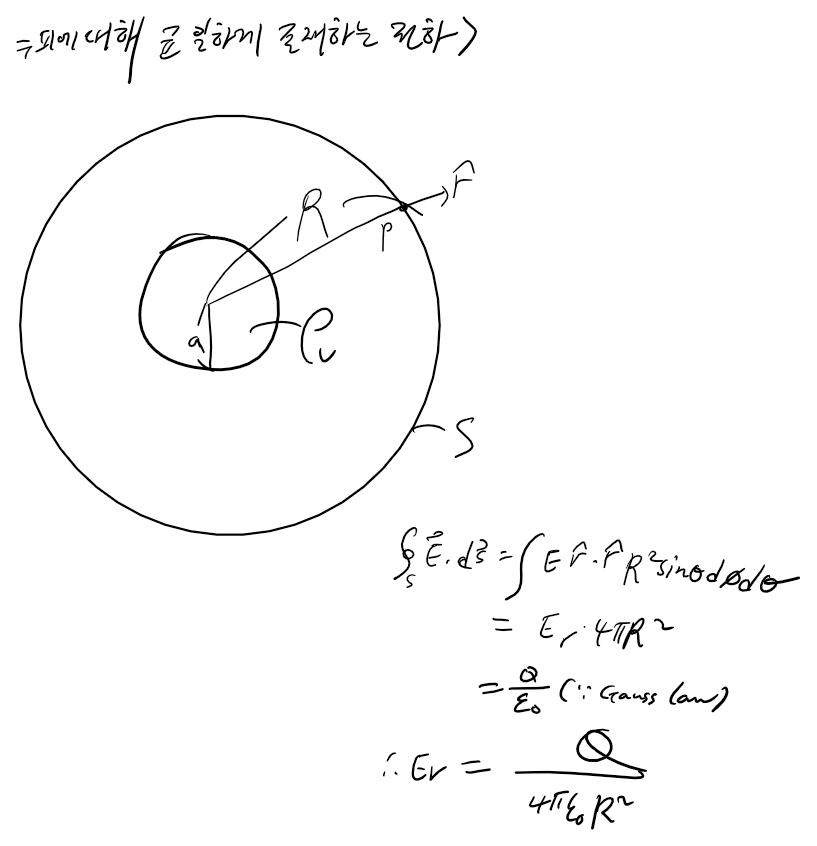
아래의 그림은 구의 중심에 전하가 하나 있는 경우입니다. 쿨롱의 법칙으로 계산이 가능한데, 반대로 가우스 법칙을 통해 쿨롱의 법칙을 유도해낼 수도 있습니다. 계산은 간단합니다. 구 좌표계에서의 dS을 알기 떄문에 식에 대입만하면 됩니다.
단 전기력이 조금 복잡한데 이걸 대칭성을 이용하여 간단하게 만들 수 있습니다. 그러니까 점 p에서 source인 전하가 가하는 전기력이 r방향으로만 작용한다는 것을 대칭성을 이용해 미리 알아둘 수 있습니다. 그러면 전기력의 성분이 하나만 남아서 계산이 용이해집니다.
직관적으로도 r방향으로만 작용할 것이라는 것은 알 수 있는데 대칭성을 이용하면, 만약 p에 작용하는 전기력이 다른 성분을 가지게 된다면 source는 변하지 않는데 전기력이 계속 변할 수는 없기 때문에 다른 성분을 가질 수 없다는 것을 알 수 있습니다.
만약 r이외의 성분을 갖는다면 source는 변하지 않는데 p에 작용하는 전기력이 원뿔의 옆면 위의 어떤 방향도 가능하기 때문에 말이 안되는 상황이 발생합니다.
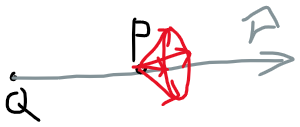
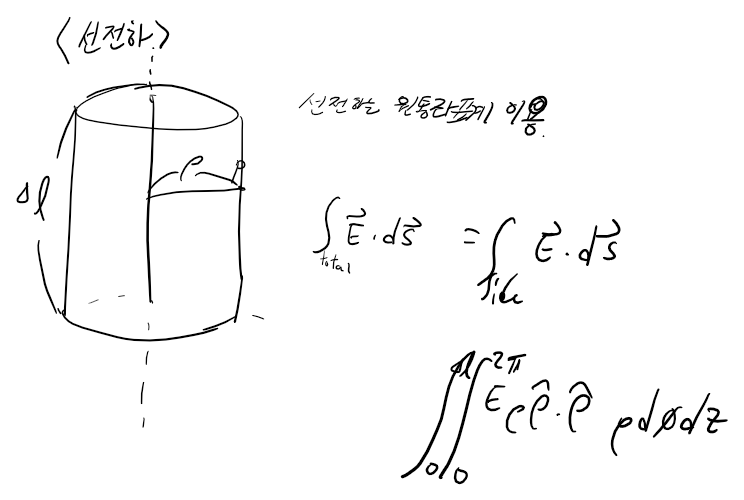
[선 전하]
선 전하도 대칭성( 또는 z나 phi성분이 서로 상쇄될 것이라는 점)을 이용하면 ρ방향 성분만 남습니다.
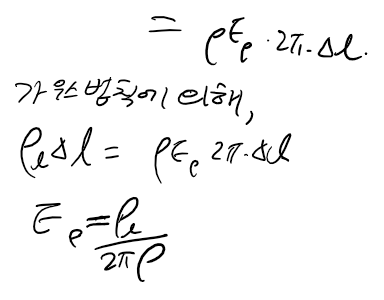
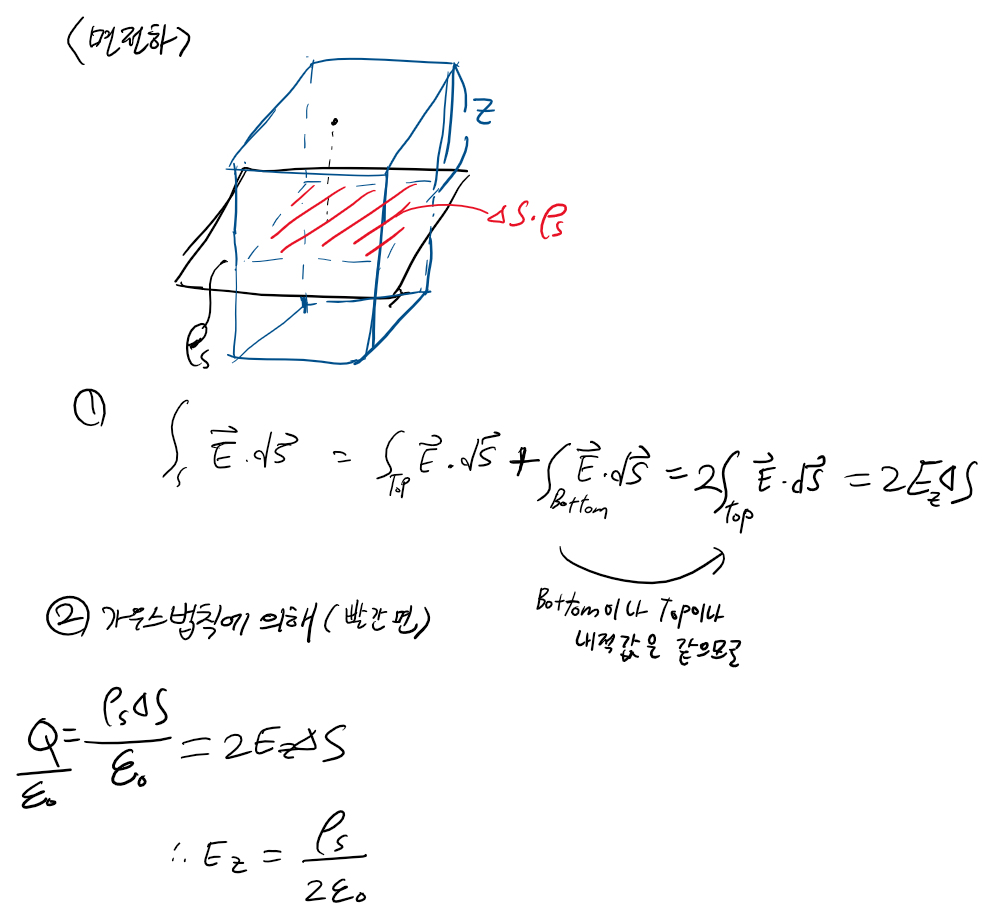
[면 전하]
[부피 전하]
'전자기학 1' 카테고리의 다른 글
| 전기장과 전위의 관계 (1) | 2023.02.22 |
|---|---|
| 전위(Electric potential) (0) | 2023.02.21 |
| 전기력 계산 (0) | 2023.02.21 |
| Laplace operator(Laplacian, 라플라시안) (0) | 2023.02.20 |
| Curl (회전) (0) | 2023.02.19 |




