전류가 흐르는 직선 도선 주위에는 자기장이 형성됩니다.

위와 같이 도선의 한 지점을 중심으로 하는 동심원을 그리는 형태입니다. 도선은 길고, 또 편의상 도선이 무한하다고 하는 경우 원통과 같은 형태로 자기장이 형성될 것입니다. 그런데 이러한 자기장을수식으로 표현할 때 직교좌표계로는 식이 복잡해집니다.
아래와 같이 임의의 점에서 자기장의 방향이 표현됩니다. 원통 좌표계에 비해 직교 좌표계가 식이 더 복잡합니다.

z축 방향의 성분은 없으므로 아래와 같이 2차원 평면에서의 방향을 찾는 것으로 간단하게 생각해 볼 수 있습니다.
x축방향 반대방향으로 가는 성분과 y축 방향으로 가는 성분의 합으로 자기장의 방향이 표현됩니다.

<원통 좌표계>
원통좌표계는 아래와 같이 ρ, φ, Z의 성분으로 나타냅니다.

직교좌표계 상에서 z축까지의 거리가 ρ, x축 거리로부터의 각도가 φ, xy평면으로부터의 거리가 z입니다.
<위치 벡터 변환>
위치 벡터 변환은 삼각함수를 이용하여 간단하게 할 수 있습니다. 임의의 점이 어느 위치에 있는지가 좌표계마다 다른데 이를 변환하는 방법입니다.
[직교 -> 원통 좌표계]
ρ = √x^2 +y^2, φ = arctan(y/x), z=z

[원통 -> 직교 좌표계]

<단위 벡터 변환>
임의의 점에서의 벡터를 표현하는 표현간의 변환입니다. 임의의 점에서 특정한 방향으로 나가는 방향을 표현하는 방식이 좌표계마다 다르므로 이를 변환하는 것입니다.
[직교 -> 원통 좌표계]


[원통 -> 직교 좌표계]
역행렬로 구할 수 있습니다.
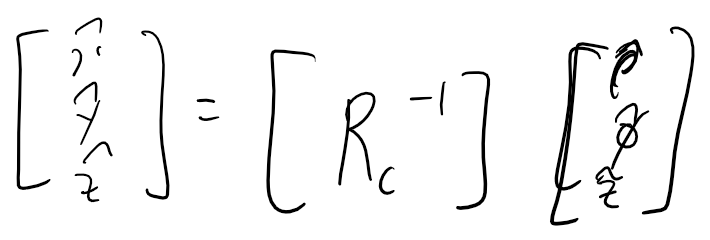
<벡터의 성분간 변환>
아래와 같이 각 좌표계에서의 벡터식을 위에서 구한 ρ, φ, Z성분과 x,y,z성분간의 관계를 이용하여 구할 수 있습니다.
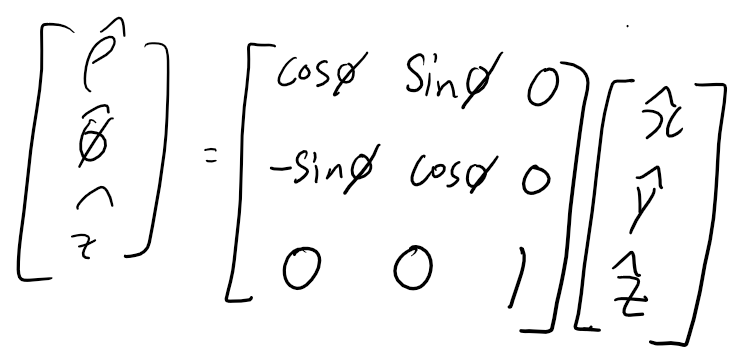
단위 벡터간 변환 단계에서 위의 행렬식 관계를 구할 수 있었습니다. 이를 아래 식에 대입하면 빨간 밑줄 부분 처럼 관계를 찾을 수 있습니다.
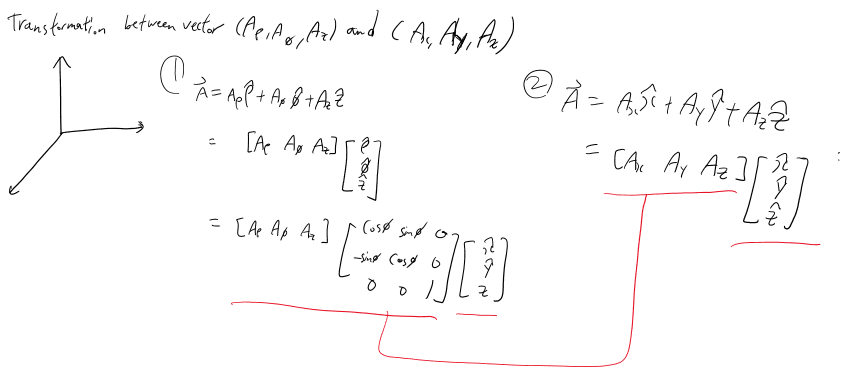
참고자료:
EM1-Lecture02-Coordinate System - YouTube
'전자기학 1' 카테고리의 다른 글
| Divergence(다이버전스, 발산) (0) | 2023.02.16 |
|---|---|
| Directional derivative(방향 도함수) (0) | 2023.02.16 |
| Differential Length, Area and Volume (0) | 2023.02.16 |
| 전자기학1 - spherical coordinate(구 좌표계) (0) | 2023.02.06 |
| 전자기학1 - Vector Algrbra(벡터 대수학) (0) | 2023.02.04 |



